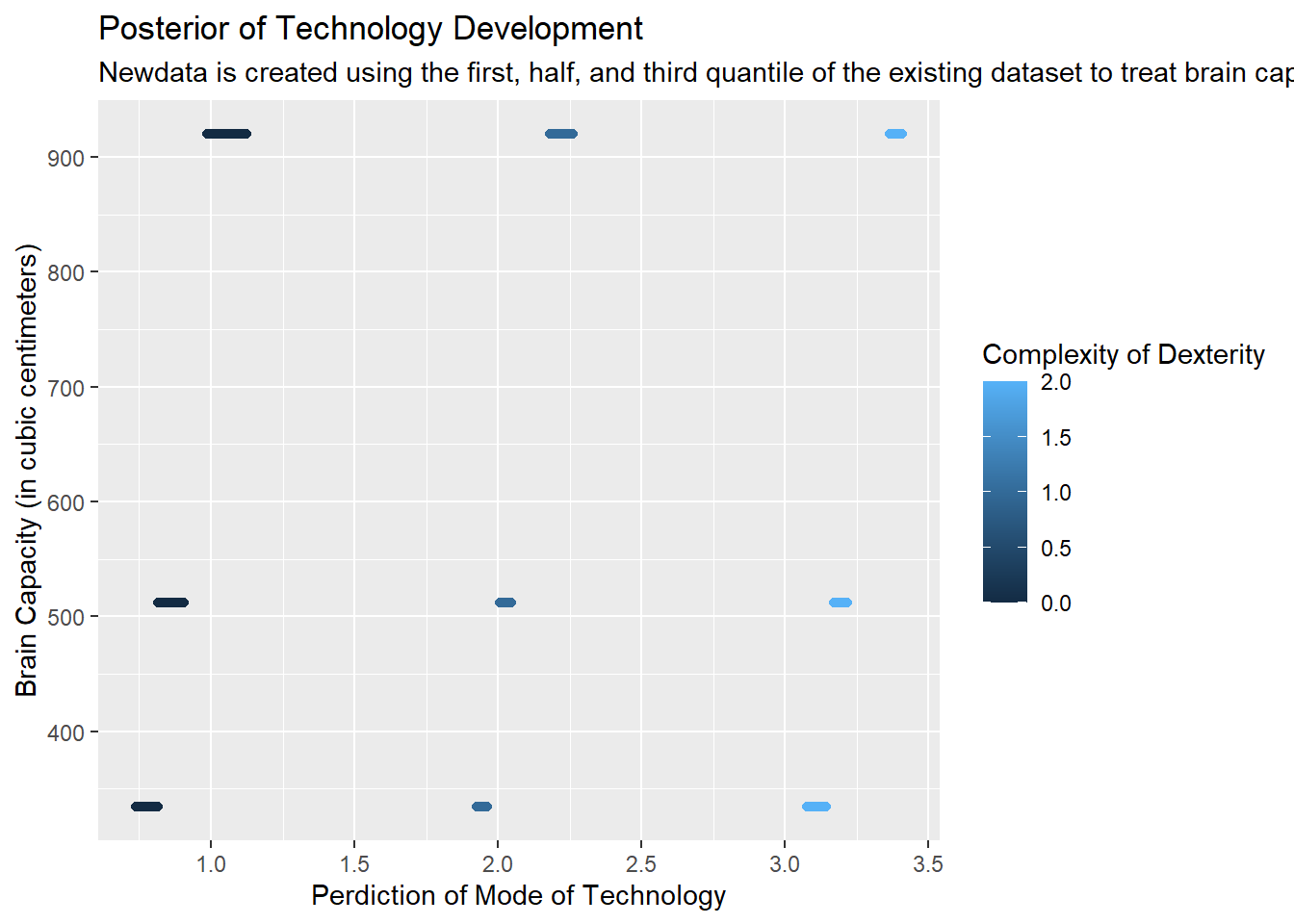
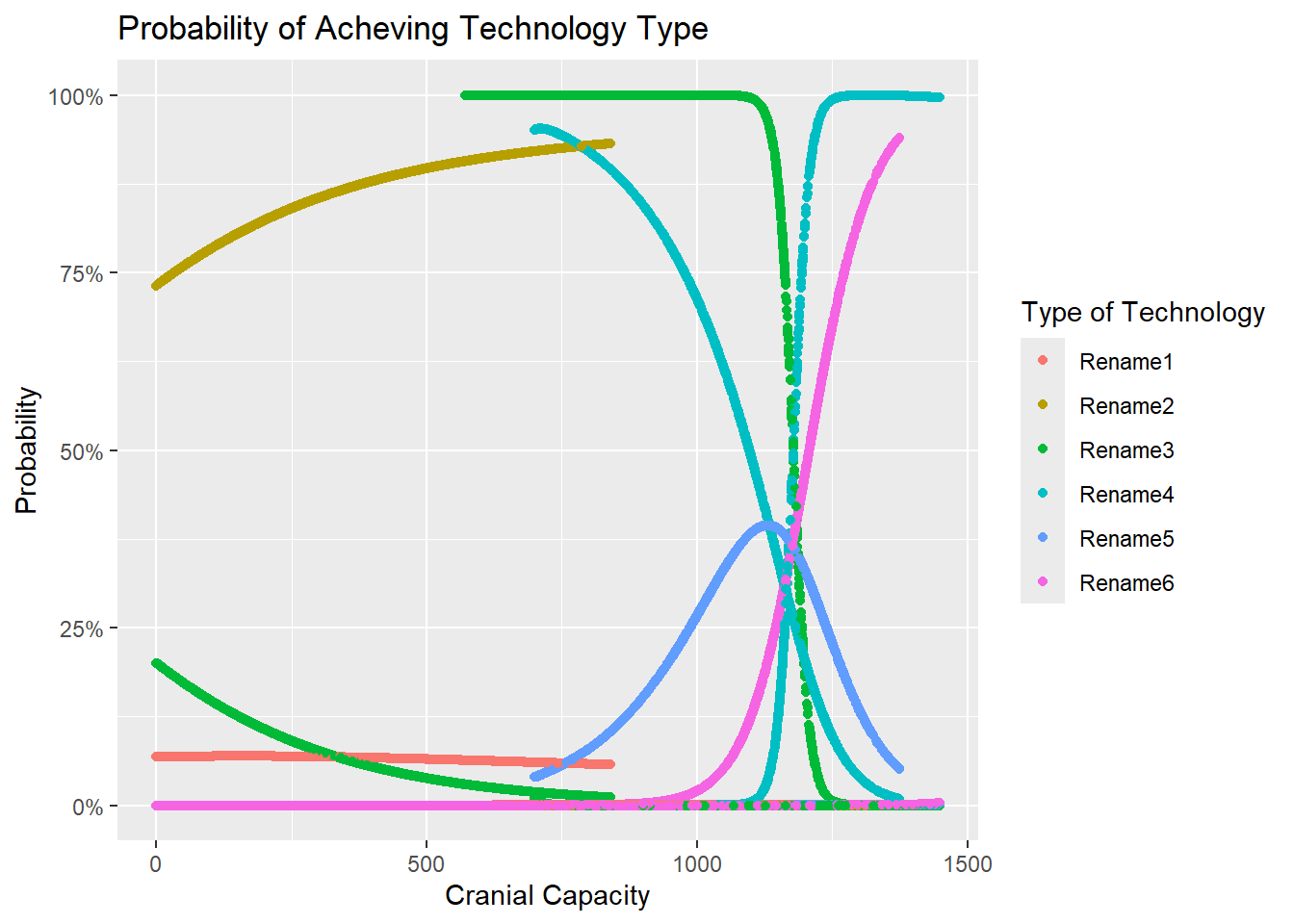
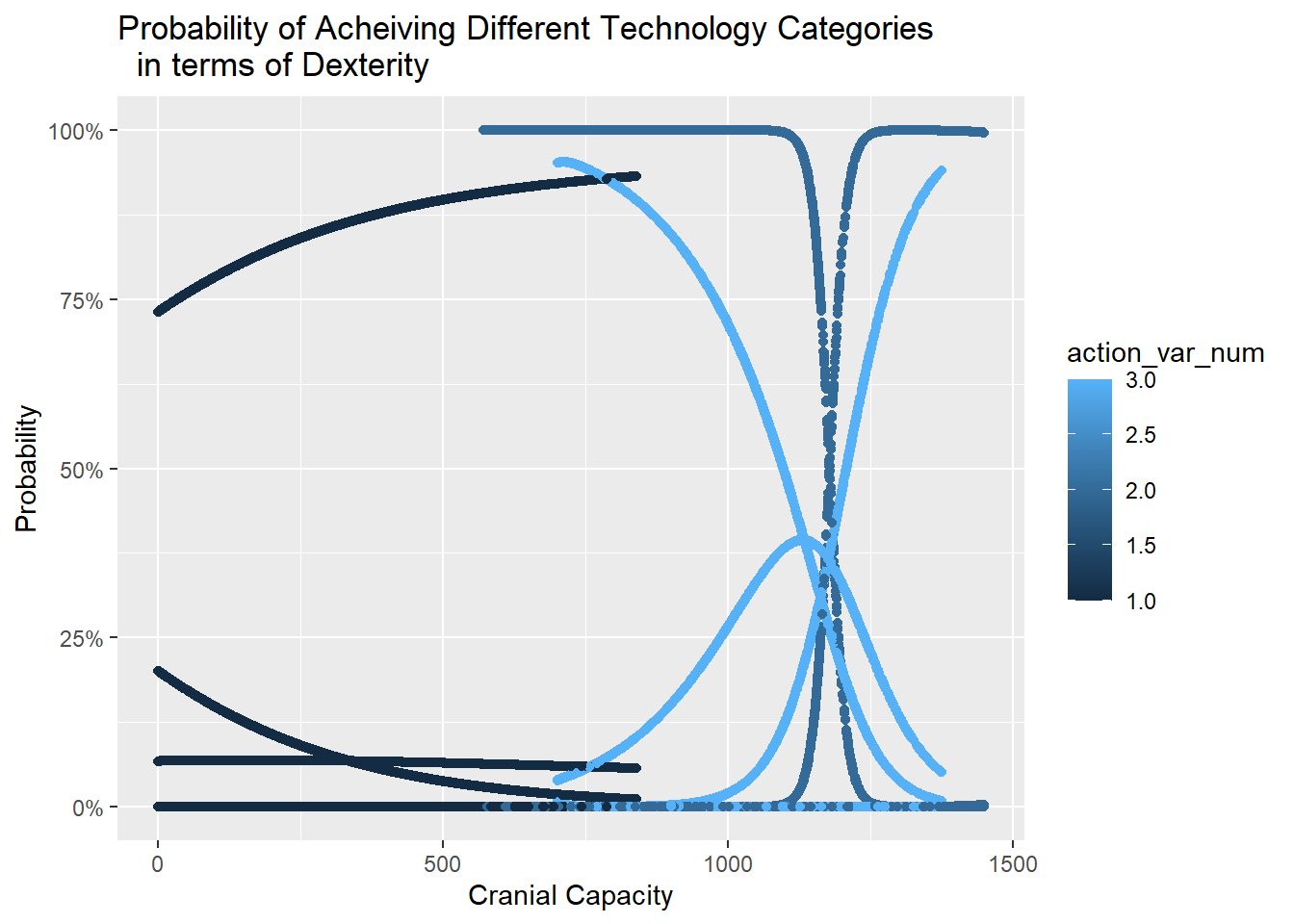
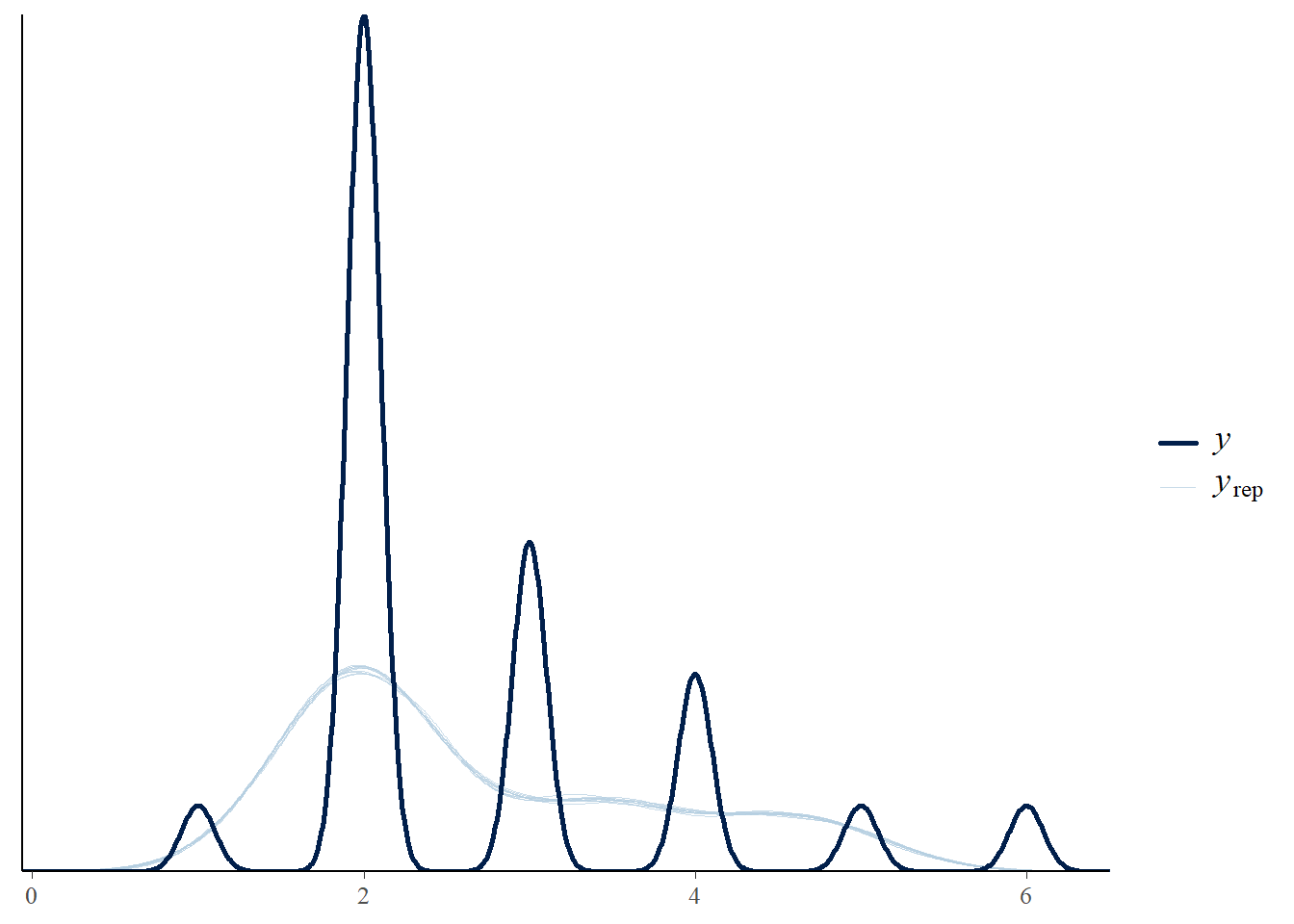
Nithura
The mathematical models used are the Gaussian model and the categorical model.
Gaussian:
Categorical:
\[ \text{Technology Amount} = \beta_0 + \beta_1 \cdot \text{Cranial Capacity} + \beta_2 \cdot \text{Manual Dexterity} + \epsilon \]
\[ \log \left( \frac{P(\text{Intermediate})}{P(\text{Simple})} \right) = \beta_{0,\text{Intermediate}} + \beta_{1,\text{Intermediate}} \cdot \text{Cranial Capacity} + \beta_{2,\text{Intermediate}} \cdot \text{Manual Dexterity} \]
\[ \log \left( \frac{P(\text{Complex})}{P(\text{Simple})} \right) = \beta_{0,\text{Complex}} + \beta_{1,\text{Complex}} \cdot \text{Cranial Capacity} + \beta_{2,\text{Complex}} \cdot \text{Manual Dexterity} \]



Characteristic |
Beta |
95% CI 1 |
|---|---|---|
| Cranial_Capacity | 0.00 | 0.00, 0.00 |
| action_var_num | 1.2 | 1.1, 1.2 |
| 1
CI = Credible Interval |
||